Aufgabenbeispiele von Vektorrechnung
Durch Aktualisieren des Browsers (z.B. mit Taste F5) kann man neue Beispielaufgaben sehen
Vektor auf Punkt addieren
Beispiel:
Der Vektor = verschiebt den Punkt P auf den Punkt Q. Gib die Koordinaten von Q an.
Wenn der Punkt P mit dem Vektor = verschoben wird, so wird ja die
x1-Kooridnate um -2, die x2-Kooridnate um 3 und die x3-Kooridnate um
-3 verschoben. Es gilt also
Q(-2
Vektor auf Punkt addieren (rw.)
Beispiel:
Der Vektor = verschiebt den Punkt P auf den Punkt Q. Gib die Koordinaten von P an.
Wenn der Punkt Q durch den Vektor = verschoben worden ist, so muss ja beim
Ausgangspunkt P jeweils die x1-Kooridnate um 5, die x2-Kooridnate um 3 und die
x3-Kooridnate um 4 kleiner gewesen sein, als bei Q. Es gilt also
P(-5 -
Vektor zwischen zwei Punkten
Beispiel:
Bestimme die Koordinaten des Vektors der den Punkt P auf den Punkt Q abbildet.
Um vom Punkt P zum Punkt Q zu gelangen, mus...
- ... in x1-Richtung die Differenz der x1-Werte, also 4-
( - 3 ) - ... in x2-Richtung die Differenz der x2-Werte, also -1-
( - 3 ) - ... in x3-Richtung die Differenz der x3-Werte, also 0-
( - 5 )
gegangen werden. Es gilt also = =
Vektorkette erkennen
Beispiel:
Der Vektor verschiebt den Punkt A auf den Punkt E.
Stelle durch die Vektoren , dar:
Wir gehen einfach vom Punkt A zum Punkt E entlang der Vektoren.
Wenn wir in Pfeilrichtung gehen, nehmen wir hierfür einfach den Vektor, wenn wir gegen die Pfeilrichtung gehen müssen, nehmen wir den Gegenvektor, also den Vektor mit einem negativen Vorzeichen:
= - +3⋅
Endpunkt von Vektorkette finden
Beispiel:
Der Vektor verschiebt den Punkt E auf den Punkt A.
Berechne mithilfe der in der Skizze rechts eingezeichneten Vektoren = , = , = , = die Koordinaten des Punkts A.
Wir gehen einfach vom Punkt E zum Punkt A entlang der Vektoren.
Wenn wir in Pfeilrichtung gehen, nehmen wir hierfür einfach den Vektor, wenn wir gegen die Pfeilrichtung gehen müssen, nehmen wir den Gegenvektor, also den Vektor mit einem negativen Vorzeichen:
= + - -
= + - -
= - -
= -
=
Jetzt müssen wir den Vektor eben noch auf den Ortsvektor von E draufaddieren:
= +
= + =
Somit gilt: A.
Vektor in Vektorkette finden
Beispiel:
Der Vektor verschiebt den Punkt A auf den Punkt F .
Berechne mithilfe der in der Skizze rechts eingezeichneten Vektoren , = , = die Koordinaten des Vektors .
Da die Koordinaten von A und F gegeben sind, können wir die Koordinaten des Verbindungsvektor (in der Skizze rechts in grau eingezeichnet) berechnen:
= =
Wenn wir nun die Vektorkette = 3⋅ + - von A nach F durchlaufen und dann den direkten Weg wieder zurück gehen, landen wir ja wieder am Aufgangspunkt A, das heißt, wir haben effektiv den Nullvektor zurückgelegt:
3⋅ + - + = |
Wenn wir nun den gesuchten Vektor auf die andere Seite bringen erhalten wir:
- + =
- + =
+ =
=
Jetzt kennen wir den Vektor für
Somit gilt: = .
Länge eines Vektors (ganzzahlig)
Beispiel:
Bestimme die Länge des Vektors = .
Für die Länge dieses Vektors gilt:
=
Länge eines Vektors
Beispiel:
Bestimme die Länge des Vektors
Für die Länge dieses Vektors
Abstand zwischen zwei Punkten berechnen
Beispiel:
Bestimme den Abstand der beiden Punkte
A
d=|
4. Punkt eines Parallelogramms
Beispiel:
Das Dreieck ABC mit A
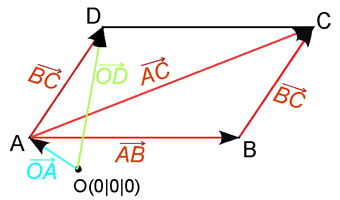 Wir sehen in der Skizze, dass man den Verbindungsvektor zwischen B und C zum Ortsvektor von A addieren muss,
um den Ortsvektor von D zu erhalten:
Wir sehen in der Skizze, dass man den Verbindungsvektor zwischen B und C zum Ortsvektor von A addieren muss,
um den Ortsvektor von D zu erhalten:
Schwerpunkt eines Dreiecks
Beispiel:
In jedem Dreieck schneiden sich die drei Verbindungslinien zwischen einem Seitenmittelpunkt und dem gegenüberliegenden Punkt im Schwerpunkt. Dabei teilen sich diese Schwerelinien immer im Verhältnis 2:1, d.h. die Strecke vom Schwerpunkt zu Eckpunkt ist doppelt so lang wie die zum Seitenmittelpunkt.
Bestimme den Schwerpunkt des Dreiecks ABC mit A
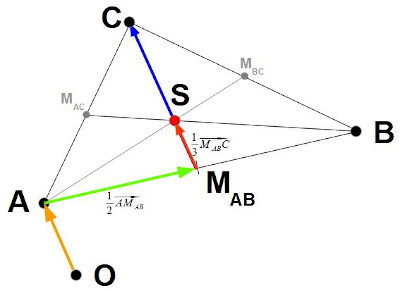 Wir sehen in der Skizze, dass wir - um den Ortsvektor
Wir sehen in der Skizze, dass wir - um den Ortsvektor
Es gilt also:
Um diese Vektoren und damit den Ortsvektor des Schwerpunkts S berechnen zu können, brauchen wir MAB, den Mittelpunkt zwischen A und B.
Hierfür können wir ja einfach in jeder Koordinate den Mittelwert bilden: .
Damit gilt für
Dies können wir nun in die obige Vektorgleichung einsetzen:
=
=
=
Die Koordinaten des gesuchten Schwerpunkts sind somit S
Fläche eines gleichschenkl. Dreiecks
Beispiel:
Gegeben ist das Dreieck ABC mit A
Zeige, dass das Dreieck gleichschenklig ist und berechne den Flächeninhalt des Dreiecks.
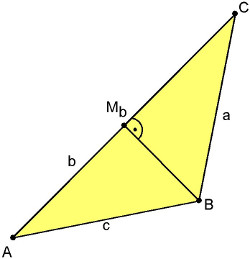
Wir berechnen zuerst einmal die drei Verbindungsvektoren jeweils zwischen zwei Punkten:
Jetzt schauen wir uns die Längen der drei Vektoren an:
c=|
b=|
a=|
Da |
Die Höhe hb trifft also genau in der Mitte auf AC.
Wir berechnen also den Mittelpunkt Mb.
Der Verbindungsvektor
Die Länge der Höhe ist |
Für den Flächeninhalt gilt also:
A=

