Aufgabenbeispiele von Anwendungen
Durch Aktualisieren des Browsers (z.B. mit Taste F5) kann man neue Beispielaufgaben sehen
Sinus und Thaleskreis (leicht)
Beispiel:
Das große Dreieck ist gleichschenklig.
Der blaue Halbkreis hat einen Durchmesser von u = 5.5 cm.
Die Länge der gemeinsamen Kante der beiden Dreiecke beträgt v = 4.7 cm.
Bestimme die fehlende Winkelweite α.
Am blauen Thaleskreis erkennt man sofort, dass γ ein rechter Winkel sein muss.
Nach der Definition des Sinus gilt im rechtwinkligen Dreieck sin(β)=
Damit folgt sin(β)==0.855 und somit β=58.7°
Wegen der Winkelsumme im Dreieck muss gelten: 90° + β + φ = 180°.
Somit gilt φ = 90° - β° = 31.3°.
Wegen der Gleichschenkligkeit des großen Dreiecks muss nun aber β und (α+φ) gleich groß sein.
Mit α+31.3°=β=58.7° gilt nun: α = 27.4°
Sinus und Thaleskreis (schwer)
Beispiel:
Das große Dreieck ist gleichschenklig. Bestimme die Länge der Strecke PQ.
Am blauen Thaleskreis über dem ersten Dreieck erkennt man sofort, dass γ ein rechter Winkel sein muss.
Aufgrund der Winkelsumme im ersten Dreieck folgt β + γ + 31° = 180°.
Daraus folgt β = 180° - 90° - 31° = 59°
Mit Hilfe des Sinus kann man nun die Länge der gemeinsamen Seite g der beiden Dreiecke berechnen:
Da g die Gegenkathete von β ist, gilt: sin(β)=sin(59°) =
Damit folgt g = sin(59°) ⋅ 5.5cm ≈ 4.7cm
Als Nebenwinkel von γ muss natürlich auch δ ein rechter Winkel sein.
Aufgrund der Gleichschenkligkeit des großen Dreiecks muss β und (α+31°) gleich groß sein. Damit gilt 59° = α + 31°, woraus folgt: α = 28°
Mit der Winkelsumme im zweiten Dreieck folgt nun ε = 90° - α = 90° - 28° = 62°
Nun können wir in diesem Dreieck den Sinus anwenden und so die gesuchte Seite PQ herausfinden: sin(ε)=
Setzt man die bekannten Werte ein, so folgt sin(62°)=
Damit folgt: PQ = ≈ 5.3cm
Trigonometrie Anwendungen
Beispiel:
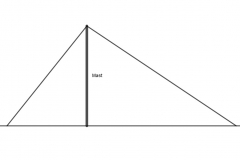
Ein 13m hoher Mast wird von der einen Seite mit einem 29m langen Seil und von der gegenüberleigenden Seite mit einem 26m langen Seil abgespannt. Wie weit sind die Verankerungen der Spannseile von einander entfernt?
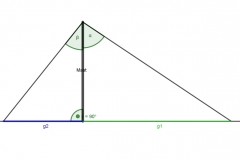
Zuerst berechnen die beiden Winkel jeweils oben in den rechtwinkligen Dreiecken:
cos(α) = = ≈ 0.4483
=> α = 63.4.
cos(β) = = ≈ 0.5
=> β = 60.
In beiden Dreiecken gilt für den Tangens: tan(α)=.
Da nach der Gegenkathete gesucht wird, stellen wir um zu
Gegenkathete g1=Ankathete ⋅ tan(α)=13 ⋅ tan(63.366881250844°)
≈25.923
Genau gleich verfahren wir mit dem anderen Dreieck:
Gegenkathete g2=Ankathete ⋅ tan(β)=13 ⋅ tan(60°)
≈22.5167
(Die Gegenkatheten hätte man auch mit dem Satz des Pythagoras berechnen können)
Die gesuchte Strecke ist nun gerade die Summe der beiden Gegenkatheten:
s=25.923 + 22.517 ≈ 48.44 m.
Winkel zw. Punkten im Koordinatensystem
Beispiel:
Berechne alle Längen und Winkel im Dreick ABC mit A(-4|1), B(3|1) und C(3|4).
Runde die Ergebnisse auf eine Nachkommastelle.
Wenn man die drei Punkte in ein Koordinatensystem einträgt erkennt man sofort, dass (zwischen B und C) a = 3 und (zwischen A und B) c = 7 sein müssen. Weil das Dreieck rechtwinklig ist, kann man b (zwischen A und C), also die Hypotenuse, mit dem Satz des Pythagoras berechnen:
Dreiecks mit Hilfe des Satzes des Pythagoras berechnen.b2 = 32 + 72
b2 = 9 + 49
b2 = 58
b = ≈ 7.62
Da a (zwischen B und C) und c (zwischen A und B) parallel zu den Koordinatenachsen sind, muss der Winkel in B β = 90° sein.
Den Winkel α können wir mit dem Tangens berechnen:
tan(α) = = ≈ 0.429
Daraus folgt: α = arctan(0.429) ≈ 23.2°.
Wegen der Winkelsumme von 180° im Dreieck folgt: γ = 90°-23.2° = 66.8°

