Aufgabenbeispiele von Pythagoras
Durch Aktualisieren des Browsers (z.B. mit Taste F5) kann man neue Beispielaufgaben sehen
Hypothenuse bestimmen (mit Pyth.)
Beispiel:
Berechne die Länge der Hypotenuse.
Im vorliegenden rechtwinkligen Dreieck sind die beiden Katheten (also die beiden Seiten, die am rechten Winkel anliegen) gegeben.
Somit kann man ganz einfach den Satz des Pythagoras anwenden:
62 + 82 = a2
36 + 64 = a2
100 = a2 |
10 = a
Die gesuchte Länge ist somit a = 10 m.
Pythagoras mit ganzen Zahlen
Beispiel:
Berechne die fehlende Länge im abgebildeten rechtwinkligen Dreieck.
Im vorliegenden rechtwinkligen Dreieck sind die beiden Katheten (also die beiden Seiten, die am rechten Winkel anliegen) gegeben.
Somit kann man ganz einfach den Satz des Pythagoras anwenden:
632 + 162 = b2
3969 + 256 = b2
4225 = b2 |
65 = b
Pythagoras mit reelen Zahlen
Beispiel:
Berechne die fehlende Länge im abgebildeten rechtwinkligen Dreieck.
Im vorliegenden rechtwinkligen Dreieck sind die beiden Katheten (also die beiden Seiten, die am rechten Winkel anliegen) gegeben.
Somit kann man ganz einfach den Satz des Pythagoras anwenden:
582 + 452 = c2
3364 + 2025 = c2
5389 = c2 |
73.41 ≈ c
Pythagoras (ohne Skizze)
Beispiel:
In einem rechtwinkligen Dreieck sind die Länge einer Kathete c = 80 cm und die Länge der Hypotenuse b = 96 cm gegeben. Berechne die Länge der anderen Kathete.
Runde auf zwei Stellen nach dem Komma.
Im vorliegenden rechtwinkligen Dreieck sind eine Kathete und die Hypotenuse (längste Seite gegenüber dem rechten Winkel) gegeben.
Somit kann man ganz einfach den Satz des Pythagoras anwenden:
802 + a2 = 962
6400 + a2 = 9216 | - 6400
a2 = 2816 |
a ≈ 53.07
Quadrate über rechtwinkl. Dreieck
Beispiel:
Berechne den Flächeninhalt der roten Fläche A.
Nach dem Satz des Pythagoras gilt:
36 + 42 = A
36 + 16 = A
52 = A
Der gesuchte Flächeninhalt ist somit A = 52 m2.
Flächeninhalt eines rechtwinkl. Dreiecks
Beispiel:
Berechne den Flächeninhalt des abgebildeten rechtwinkligen Dreiecks.
Als erstes berechnen wir die Länge der anderen Kathete:
Im vorliegenden rechtwinkligen Dreieck sind eine Kathete und die Hypotenuse (längste Seite gegenüber dem rechten Winkel) gegeben.
Somit kann man ganz einfach den Satz des Pythagoras anwenden:
802 + c2 = 892
6400 + c2 = 7921 | - 6400
c2 = 1521 |
c = 39
Da im rechtwinkligen Dreieck ja immer die eine Kathete gleichzeitig die Höhe auf der andere Kathete ist, kann man den Flächeninhalt ganz einfach berechnen als:
A = ⋅ 39 cm ⋅ 80 cm
also A = 1560 cm2
Pythagoras im Rechteck und Dreieck
Beispiel:
Berechne die fehlende Länge a im abgebildeten Dreieck.
Runde das Ergebnis auf zwei Nachkommastellen.
Im vorliegenden gleichschenkligen Dreieck teilt die Höhe das Dreieck in zwei kongruente Hälften. Bei diesen beiden Teildreiecken ist demnach also jeweils die untere waagrechte Seite 5 cm lang.
In einem dieser beiden rechtwinkligen Dreiecke können wir mit Hilfe des Satzes des Pythagoras die fehlende Strecke a berechnen.
52 + 42 = a2
25 + 16 = a2
41 = a2 |
a = ≈ 6.4
Die gesuchte Länge ist somit a ≈ 6.4 cm.
Pyth. im Rechteck und Dreieck (ohne Skizze)
Beispiel:
In einem Rechteck sind die beiden Seitenlängen mit a=6 cm und b=7 cm gegeben. Berechne die Länge der Diagonalen des Rechtecks.
Runde das Ergebnis auf zwei Nachkommastellen.
Im vorliegenden Rechteck sind teilt die rote Diagonale das Rechteck in zwei (kongruente) Dreiecke. In einem dieser beiden rechtwinkligen Dreiecke können wir mit Hilfe des Satzes des Pythagoras die fehlende Strecke d berechnen.
62 + 72 = d2
36 + 49 = d2
85 = d2 |
d = ≈ 9.22
Die gesuchte Länge ist somit d ≈ 9.22 cm.
Pythagoras rückwärts
Beispiel:
Gegeben ist ein gleichseitiges Dreieck mit der Höhe h=7 m Berechne die Seitenlänge a dieses gleichseitigen Dreieck.
Runde das Ergebnis auf zwei Nachkommastellen.
Mit Hilfe des Satzes des Pythagoras können wir die Höhe im gleichseitigen Dreieck in Abhängigkeit von der Seitenlänge a ausdrücken. Dabei gilt:
+ h2 = a2
+ h2 = a2 | -
h2 = a2 |
h =
= a |⋅
oder eben a =
Somit gilt in unserem Fall:
a =
Pythagoras rückwärts (schwer)
Beispiel:
Gegeben ist ein Rechteck mit der Diagonalenlänge d=82 mm und dem Umfang 196 mm.
Berechne den Flächeninhalt des Rechtecks.
Wenn wir die beiden Seitenlängen des Rechtecks a und b nennen, gilt für den Umfang:
I: U=2⋅a + 2⋅b
Außerdem können wir mit Hilfe des Satzes des Pythagoras die Länge der Diagonalen eines Rechtecks in Abhängigkeit von a und b ausdrücken. Dabei gilt:
II: a2 + b2 = d2
Konkret in dieser Aufgabe bedeutet das:
I: 196=2⋅a + 2⋅b | :2
II: a2 + b2 = 822
vereinfacht
I: 98=a + b
II: a2 + b2 = 6724
Wenn wir nun die erste Gleichung nach b auflösen erhalten wir
I: b = 98 - a
II: a2 + b2 = 6724
Jetzt setzen wir das b in Gleichung I in die Gleichung II ein:
II: a2 + (98 - a)2 = 6724
Durch Ausmultiplizieren mit der binomischen Formel erhalten wir:
|
|
= |
|
|
|
|
= |
|
|
|
eingesetzt in die Mitternachtsformel (a-b-c-Formel):
a1,2 =
a1,2 =
a1,2 =
a1 =
a2 =
Man kann erkennen, dass die Summe der beiden Lösungen gerade wieder den halben Umfang ergibt (vergleiche Gleichung I oben)
(I) 98 = 80 + 18
Das bedeutet, dass die beiden Lösungen gerade die beiden gesuchten Seitenlängen des Rechtecks sind.
Jetzt ist der Flächeninhalt des Rechtecks leicht zu berechnnen:
A = a ⋅ b = 80 mm ⋅ 18 mm = 1440 mm2
Abstand zweier Punkte
Beispiel:
Berechne den Abstand der beiden Punkte A(3|3) und B(0|5) im Koordinatensystem.
Runde das Ergebnis auf zwei Nachkommastellen.
Wie man in der Skizze rechts gut erkennen kann, lässt sich der Abstand zwischen zwei Punkten als Hypotenuse eines rechtwinkligen Dreiecks mit Hilfe des Satzes des Pythagoras berechnen.
Dabei ist die Länge der waagrechten Kathete gerade die Differenz der x-Werte der beiden Punkte:
dx =
3 -
Und die Länge der senkrechten Kathete ist die Differenz der y-Werte der beiden Punkte:
dy =
5 -
Jetzt können wir den Satz des Pythagoras anwenden:
d2 = 32 + 22
d2 = 9 + 4
d2 = 13
d =
Für den Abstand der beiden Punkte gilt also: d ≈ 3.61
Anwendungen Pythagoras
Beispiel:
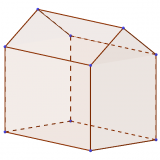
Ein Haus hat eine Gesamthöhe von 11,5m. Die (fünfeckigen) Stirnseiten sind 8m breit. Die rechteckigen Seitenflächen sind 13m lang und vom Boden bis zur Dachkante 9m hoch. Berechne die Fläche des Hausdachs.
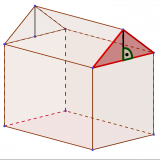
Es gilt:
2.52 + 42 =h2
6.25 +16 = h2
22.25 = h2 |
4.72 ≈ h
Um die gesuchte Fläche zu berechnen, muss nun zunächst diese Hypotenuse mit 13m multipliziert werden.
Somit erhalten wir für eine Hälfte der gesuchten Fläche: AH ≈ 61.32m2
Für die Gesamtfläche gilt dann:
A ≈ 122.64m2

