Aufgabenbeispiele von Winkel
Winkel zwischen zwei Vektoren
Beispiel:
Berechne den Winkel zwischen den Vektoren = und =
Lösung einblenden
Wir bilden
(wie immer bei Winkeln) das Sklarprodukt der beiden Vektoren, also von und
und teilen dieses durch die Längen der Vektoren.
Der Betrag des normierten Skalarprodukts ist gleich dem cos des gesuchten Winkels zwischen den Ebenen.
 Wir berechnen den Winkel zwischen
den Vektoren =
und =
Wir berechnen den Winkel zwischen
den Vektoren =
und =
also α ≈120.3°
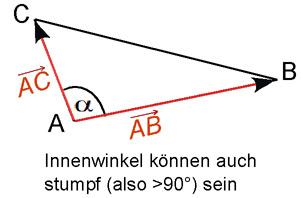
Innenwinkel im Dreieck
Beispiel:
Gegeben ist das Dreieck ABC mit A(-1|4|2), B(-5|8|6) und C(2|7|7). Berechne den Innenwinkel des Dreiecks im Punkt A.
Lösung einblenden
 Wir berechnen den Winkel zwischen
den Vektoren
AB
→
=
(
-4
4
4
)
und
AC
→
=
(
3
3
5
)
Wir berechnen den Winkel zwischen
den Vektoren
AB
→
=
(
-4
4
4
)
und
AC
→
=
(
3
3
5
)
cos(α)=
AB
→
⋅
AC
→
|
AB
→
|⋅|
AC
→
|
=
(-4)⋅3 +
4⋅3 +
4⋅5
(-4) 2
+
42
+
4 2
⋅
3 2
+
32
+
5 2
=
20
48 ⋅ 43
≈ 0.4402also α ≈63.9°
Winkel zwischen 2 Geraden
Beispiel:
Berechne den Winkel unter dem sich die Geraden
g: x → = ( -1 5 -5 ) +t⋅ ( -5 -3 -4 ) und h: x → = ( 9 11 3 ) +t⋅ ( -5 5 5 ) schneiden.
Lösung einblenden
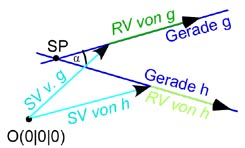
Wir bilden (wie immer bei Winkeln) das Sklarprodukt von den Richtungsvektoren der beiden Geraden, also von
(
-5
-3
-4
)
und
(
-5
5
5
)
, und teilen dieses durch die Längen der Vektoren. (Um immer den kleineren der beiden Schnittwinkel α
und (180°-α) zu erhalten, muss davon immer noch der Betrag genommen werden.)
Der Betrag des normierten Skalarprodukts ist gleich dem cos des gesuchten Winkels zwischen den sich schneidenden Geraden.
cos(α) =
|
(
-5
-3
-4
)
⋅
(
-5
5
5
)
|
|
(
-5
-3
-4
)
|
⋅
|
(
-5
5
5
)
|
=
|
(-5)⋅(-5) +
(-3)⋅5 +
(-4)⋅5
|
(-5) 2
+
(-3)2
+
(-4) 2
⋅
(-5) 2
+
52
+
5 2
=
|
-10
|
50
⋅
75
≈
0.1633
also Schnittwinkel α ≈ 80.6°
Winkel zwischen 2 Ebenen
Beispiel:
Berechne den Winkel zwischen den Ebenen
E: 3 x 1 + x 2 +6 x 3 = 12 und F: x 1 +4 x 2 +4 x 3 = -4
Lösung einblenden
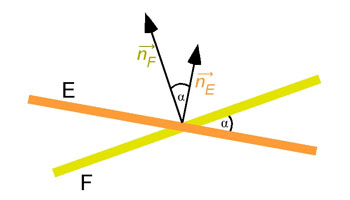 Wir bilden
(wie immer bei Winkeln) das Sklarprodukt von den Normalenvektoren der beiden Ebenen, also von
(
3
1
6
)
und
(
1
4
4
)
, und teilen dieses durch die Längen der Vektoren. (Um immer den kleineren der beiden Schnittwinkel α
und (180°-α) zu erhalten, muss davon immer noch der Betrag genommen werden.)
Wir bilden
(wie immer bei Winkeln) das Sklarprodukt von den Normalenvektoren der beiden Ebenen, also von
(
3
1
6
)
und
(
1
4
4
)
, und teilen dieses durch die Längen der Vektoren. (Um immer den kleineren der beiden Schnittwinkel α
und (180°-α) zu erhalten, muss davon immer noch der Betrag genommen werden.)
Der Betrag des normierten Skalarprodukts ist gleich dem cos des gesuchten Winkels zwischen den Ebenen
(weil dieser ja gleich ist, wie der zwischen den Normalenvektoren).
cos(α) =
|
(
3
1
6
)
⋅
(
1
4
4
)
|
|
(
3
1
6
)
|
⋅
|
(
1
4
4
)
|
|
3⋅1 +
1⋅4 +
6⋅4
|
3 2
+
12
+
6 2
⋅
1 2
+
42
+
4 2
=
|
31
|
46
⋅
33
≈
0.7957also Schnittwinkel α ≈ 37.3°
Winkel zwischen Ebene und Gerade
Beispiel:
Berechne den Winkel zwischen der Ebene
E: 5 x 1 -2 x 2 +2 x 3 = 10 und der Geraden g: x → = ( 0 0 -3 ) +t⋅ ( -3 -5 -5 )
Lösung einblenden
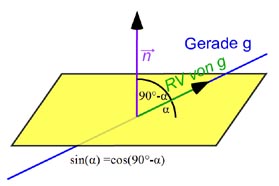
Wir bilden (wie immer bei Winkeln) das Sklarprodukt,
diesesmal von Normalenvektor der Ebene
(
5
-2
2
)
mit dem Richtungsvektor der Geraden
(
-3
-5
-5
)
, und teilen dieses durch die Längen der Vektoren. (Um immer den kleineren der beiden Schnittwinkel α
und (180°-α) zu erhalten, muss davon immer noch der Betrag genommen werden.)
Da wir so ja eigentlich den Winkel zwischen Normalenvektor und Gerade berechnen würden, müssen wir das diesesmal = sin(α) setzen.
sin(α) =
|
(
5
-2
2
)
⋅
(
-3
-5
-5
)
|
|
(
5
-2
2
)
|
⋅
|
(
-3
-5
-5
)
|
=
|
5⋅(-3) +
(-2)⋅(-5) +
2⋅(-5)
|
5 2
+
(-2)2
+
2 2
⋅
(-3) 2
+
(-5)2
+
(-5) 2
=
|
-15
|
33
⋅
59
≈
0.3399
also Schnittwinkel α ≈ 19.9°
Winkel zwischen 2 Ebenen
Beispiel:
Berechne den Winkel zwischen den Ebenen
E: 3 x 1 -2 x 2 -9 x 3 = -18 und F: 2 x 1 +7 x 2 +8 x 3 = -112
Lösung einblenden
 Wir bilden
(wie immer bei Winkeln) das Sklarprodukt von den Normalenvektoren der beiden Ebenen, also von
(
3
-2
-9
)
und
(
2
7
8
)
, und teilen dieses durch die Längen der Vektoren. (Um immer den kleineren der beiden Schnittwinkel α
und (180°-α) zu erhalten, muss davon immer noch der Betrag genommen werden.)
Wir bilden
(wie immer bei Winkeln) das Sklarprodukt von den Normalenvektoren der beiden Ebenen, also von
(
3
-2
-9
)
und
(
2
7
8
)
, und teilen dieses durch die Längen der Vektoren. (Um immer den kleineren der beiden Schnittwinkel α
und (180°-α) zu erhalten, muss davon immer noch der Betrag genommen werden.)
Der Betrag des normierten Skalarprodukts ist gleich dem cos des gesuchten Winkels zwischen den Ebenen
(weil dieser ja gleich ist, wie der zwischen den Normalenvektoren).
cos(α) =
|
(
3
-2
-9
)
⋅
(
2
7
8
)
|
|
(
3
-2
-9
)
|
⋅
|
(
2
7
8
)
|
|
3⋅2 +
(-2)⋅7 +
(-9)⋅8
|
3 2
+
(-2)2
+
(-9) 2
⋅
2 2
+
72
+
8 2
=
|
-80
|
94
⋅
117
≈
0.7628also Schnittwinkel α ≈ 40.3°
 Wir berechnen den Winkel zwischen
den Vektoren =
und =
Wir berechnen den Winkel zwischen
den Vektoren =
und =  Wir berechnen den Winkel zwischen
den Vektoren
Wir berechnen den Winkel zwischen
den Vektoren  Wir bilden (wie immer bei Winkeln) das Sklarprodukt von den Richtungsvektoren der beiden Geraden, also von
Wir bilden (wie immer bei Winkeln) das Sklarprodukt von den Richtungsvektoren der beiden Geraden, also von  Wir bilden
(wie immer bei Winkeln) das Sklarprodukt von den Normalenvektoren der beiden Ebenen, also von
Wir bilden
(wie immer bei Winkeln) das Sklarprodukt von den Normalenvektoren der beiden Ebenen, also von  Wir bilden (wie immer bei Winkeln) das Sklarprodukt,
Wir bilden (wie immer bei Winkeln) das Sklarprodukt,  Wir bilden
(wie immer bei Winkeln) das Sklarprodukt von den Normalenvektoren der beiden Ebenen, also von
Wir bilden
(wie immer bei Winkeln) das Sklarprodukt von den Normalenvektoren der beiden Ebenen, also von 
