Pestalozzi Gymnasium Biberach EduRandomtasks

Durchstosspunkt Anwendungen

Beispiel:

Das Dach eines Gebäudes befindet sich in der Ebene E: $x_{1} - 6 x_{2} = -12$ . Dieses soll durch eine senkrechte Säule abgestützt werden, deren unteres Ende sich im Punkt P $(-12 | 0 | 2)$ befindet. In welchem Punkt befindet sich das obere Ende der Säule am Dach?

Lösung einblenden

Gesucht ist der Durchstoßpunkt zwischen der Geraden g: $\vec{x} =$ $(\begin{matrix} -12 \\ 0 \\ 2 \end{matrix}) + t \cdot (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix})$ und der Ebene E : $x_{1} - 6 x_{2} = -12$ .

Wir setzen einen allgemeinen Geradenpunkt der Geraden $G_{t} (-12 + 0 t | 0 + 0 t | 2 + 1 t)$ in die Ebene ein und lösen nach t auf:

$1 \cdot (- 12 + 0) - 6 \cdot (0 + 0) + 0 \cdot (2 + t)$	=	$- 12$
$- 12$	=	$- 12$	\| $+ 12$
0	=	0

Diese Gleichung hat unendlich viele Lösungen!

Den Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt $G_{t} (-12 + 0 t | 0 + 0 t | 2 + 1 t)$ einsetzen.
=> D $(- 12 | 0 | 2)$ .

Einen Punkt an einer Ebene spiegeln

Beispiel:

Der Punkt $P (5 | 4 | -1)$ wird an der Ebene E: $5 x_{1} - 2 x_{2} - 4 x_{3} = -24$ gespiegelt!
Berechne den Bildpunkt P'!

Lösung einblenden

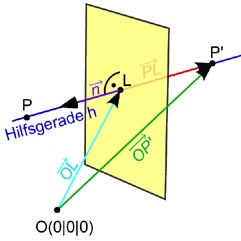Wir stellen eine Hilfsgerade durch den zu spiegelnden Punkt P (Stützvektor) mit dem Normalenvektor der Spiegelebene als Richtungsvektor auf:
h:

\vec{x} =

(\begin{matrix} 5 \\ 4 \\ -1 \end{matrix}) + t \cdot (\begin{matrix} 5 \\ -2 \\ -4 \end{matrix})

Diese Hilfsgerade h durchstößt die Spiegelebene im Lotfußpunkt
(Detail-Rechnung einblenden)

Gesucht ist der Durchstoßpunkt zwischen der Geraden g: $\vec{x} =$ $(\begin{matrix} 5 \\ 4 \\ -1 \end{matrix}) + t \cdot (\begin{matrix} 5 \\ -2 \\ -4 \end{matrix})$ und der Ebene E : $5 x_{1} - 2 x_{2} - 4 x_{3} = -24$ .

Wir setzen einen allgemeinen Geradenpunkt der Geraden $G_{t} (5 + 5 t | 4 - 2 t | -1 - 4 t)$ in die Ebene ein und lösen nach t auf:

$5 \cdot (5 + 5 t) - 2 \cdot (4 - 2 t) - 4 \cdot (- 1 - 4 t)$	=	$- 24$
$25 t + 25 + 4 t - 8 + 16 t + 4$	=	$- 24$
$45 t + 21$	=	$- 24$	\| $- 21$
$45 t$	=	$- 45$	\|: $45$
$t$	=	$- 1$

Den Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt $G_{t} (5 + 5 t | 4 - 2 t | -1 - 4 t)$ einsetzen.
=> D $(0 | 6 | 3)$ .

Der Verbindungsvektor

\vec{PL}

zwischen dem zu spiegelnden Punkt P und diesem Lotfußpunkt

L (0 | 6 | 3)

ist ein Vielfaches des Normalenvektors der Spiegelebene, also orthogonal zur Ebene. Addiert man diesen Verbindungsvektor zum Ortsvektor des Lotfußpunktes L,

\vec{OP'}

=

\vec{OL}

+

\vec{PL}

=

(\begin{matrix} 0 \\ 6 \\ 3 \end{matrix})

+

(\begin{matrix} -5 \\ 2 \\ 4 \end{matrix})

=

(\begin{matrix} -5 \\ 8 \\ 7 \end{matrix})

so erhält man den Ortsvektor des gespiegelten Bildpunktes P'.
Der gesuchte Spiegelpunkt ist also $P' (-5 | 8 | 7)$ .

Spiegel-Ebene zu zwei Punkten finden

Beispiel:

Bestimme die Spiegelebene E, die den Punkt $P (-1 | 4 | -5)$ auf $P' (-9 | -4 | 1)$ abbildet!

Lösung einblenden

Da Punkte immer orthogonal an einer Ebene gespiegelt werden, muss der Verbindungsvektor der beiden Punkte

P (-1 | 4 | -5)

und

P' (-9 | -4 | 1)

der Normalenvektor der Spiegelebene sein:

(\begin{matrix} -8 \\ -8 \\ 6 \end{matrix})

= -2⋅

(\begin{matrix} 4 \\ 4 \\ -3 \end{matrix})

.
Die Spiegelebene hat also die Gleichung:

4 x_{1} + 4 x_{2} - 3 x_{3} = d

Um 'd' noch zu berechnen, muss man den Mittelpunkt der beiden Punkte . M

(\frac{-1 + (- 9)}{2} | \frac{4 + (- 4)}{2} | \frac{-5 + 1}{2})

=

M (-5 | 0 | -2)

in diese Gleichung einsetzen.

4 \cdot (-5) + 4 \cdot 0 + (-3) \cdot (-2)

=-14=d
also ist die Koordinatengleichung der Ebene:

4 x_{1} + 4 x_{2} - 3 x_{3} = -14

Gerade an Ebene spiegeln

Beispiel:

Die Gerade $\vec{x} =$ $(\begin{matrix} 5 \\ 5 \\ 5 \end{matrix}) + t \cdot (\begin{matrix} -12 \\ -2 \\ 23 \end{matrix})$ wird an der Ebene E: $-4 x_{1} - 2 x_{2} + 12 x_{3} = 358$ gespiegelt.
Bestimme die Bildgerade g'.

Lösung einblenden

Das Spiegelbild einer Geraden ist wieder eine Gerade. Es genügt also zwei Punkte der Geraden g zu spiegeln und die Bildpunkte wieder zu einer Geraden zu verbinden.

Als ersten Punkt spiegeln wir den Aufpunkt der Geraden A $(5 | 5 | 5)$

Wir stellen eine Hilfsgerade durch den zu spiegelnden Punkt P (Stützvektor) mit dem Normalenvektor der Spiegelebene als Richtungsvektor auf:
h:

\vec{x} =

(\begin{matrix} 5 \\ 5 \\ 5 \end{matrix}) + t \cdot (\begin{matrix} -4 \\ -2 \\ 12 \end{matrix})

Diese Hilfsgerade h durchstößt die Spiegelebene im Lotfußpunkt
(Detail-Rechnung einblenden)

Gesucht ist der Durchstoßpunkt zwischen der Geraden g: $\vec{x} =$ $(\begin{matrix} 5 \\ 5 \\ 5 \end{matrix}) + t \cdot (\begin{matrix} -4 \\ -2 \\ 12 \end{matrix})$ und der Ebene E : $-4 x_{1} - 2 x_{2} + 12 x_{3} = 358$ .

Wir setzen einen allgemeinen Geradenpunkt der Geraden $G_{t} (5 - 4 t | 5 - 2 t | 5 + 12 t)$ in die Ebene ein und lösen nach t auf:

$- 4 \cdot (5 - 4 t) - 2 \cdot (5 - 2 t) + 12 \cdot (5 + 12 t)$	=	$358$
$16 t - 20 + 4 t - 10 + 144 t + 60$	=	$358$
$164 t + 30$	=	$358$	\| $- 30$
$164 t$	=	$328$	\|: $164$
$t$	=	$2$

Den Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt $G_{t} (5 - 4 t | 5 - 2 t | 5 + 12 t)$ einsetzen.
=> D $(-3 | 1 | 29)$ .

Der Verbindungsvektor

\vec{PL}

zwischen dem zu spiegelnden Punkt P und diesem Lotfußpunkt

L (-3 | 1 | 29)

ist ein Vielfaches des Normalenvektors der Spiegelebene, also orthogonal zur Ebene. Addiert man diesen Verbindungsvektor zum Ortsvektor des Lotfußpunktes L,

\vec{OP'}

=

\vec{OL}

+

\vec{PL}

=

(\begin{matrix} -3 \\ 1 \\ 29 \end{matrix})

+

(\begin{matrix} -8 \\ -4 \\ 24 \end{matrix})

=

(\begin{matrix} -11 \\ -3 \\ 53 \end{matrix})

so erhält man den Ortsvektor des gespiegelten Bildpunktes P'.
Der gesuchte Spiegelpunkt ist also $P' (-11 | -3 | 53)$ .

Theoretisch könnte man jetzt einen beliebigen zweiten Punkt spiegeln. Etwas weniger Aufwand ist es aber, einfach den Durchstoßpunkt der Geraden mit der Ebene zu berechnen, weil sich dieser ja durch die Spiegelung an der Ebene nicht ändert:

Gesucht ist der Durchstoßpunkt zwischen der Geraden g: $\vec{x} =$ $(\begin{matrix} 5 \\ 5 \\ 5 \end{matrix}) + t \cdot (\begin{matrix} -12 \\ -2 \\ 23 \end{matrix})$ und der Ebene E : $-4 x_{1} - 2 x_{2} + 12 x_{3} = 358$ .

Wir setzen einen allgemeinen Geradenpunkt der Geraden $G_{t} (5 - 12 t | 5 - 2 t | 5 + 23 t)$ in die Ebene ein und lösen nach t auf:

$- 4 \cdot (5 - 12 t) - 2 \cdot (5 - 2 t) + 12 \cdot (5 + 23 t)$	=	$358$
$48 t - 20 + 4 t - 10 + 276 t + 60$	=	$358$
$328 t + 30$	=	$358$	\| $- 30$
$328 t$	=	$328$	\|: $328$
$t$	=	$1$

Den Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt $G_{t} (5 - 12 t | 5 - 2 t | 5 + 23 t)$ einsetzen.
=> D $(-7 | 3 | 28)$ .

Damit haben wir jetzt zwei Punkte der gespiegelten Bildgeraden: Den Spiegelpunkt des Aufpunkts A' $(-11 | -3 | 53)$ und den fixen Durchstoßpunkt der Geraden mit der Ebene D $(-7 | 3 | 28)$ und wir können die Gerade durch diese beiden Punkte aufstellen:

g': $\vec{x} =$ $(\begin{matrix} -11 \\ -3 \\ 53 \end{matrix}) + t \cdot (\begin{matrix} -4 \\ -6 \\ 25 \end{matrix})$

Geradenpunkt mit d zu Ebene finden

Beispiel:

Welche Punkte auf der Geraden g mit g: $\vec{x} =$ $(\begin{matrix} -9 \\ 9 \\ 4 \end{matrix}) + t \cdot (\begin{matrix} 2 \\ -4 \\ -6 \end{matrix})$ haben von der Ebene E: $2 x_{1} - 2 x_{2} - x_{3} = -4$ den Abstand d=6?

Lösung einblenden

Wir setzen einfach einen allgemeinen Geradenpunkt

G_{t} (-9 + 2 t | 9 - 4 t | 4 - 6 t)

in die Hesse'sche Punkt-Ebene-Abstandsaformel ein:

$\frac{|2\cdot(-9+2t)-2\cdot(9-4t)-1\cdot(4-6t)+4|}{\sqrt{2^{2} + {(-2)}^{2} + {(-1)}^{2}}}$ = 6|⋅3

|-36+18t| = 18

1. Fall
-36+18t = 18|+36

18t = 54|:18

t₁ = 3

eingesetzt in die Geradengleichung: $\vec{OP1}$ = $(\begin{matrix} -9 \\ 9 \\ 4 \end{matrix}) + 3 \cdot (\begin{matrix} 2 \\ -4 \\ -6 \end{matrix})$ = $(\begin{matrix} -3 \\ -3 \\ -14 \end{matrix})$

2. Fall
-(-36+18t) = 18

36-18t = 18|-36

-18t = -18|:-18

t₂ = 1

eingesetzt in die Geradengleichung: $\vec{OP2}$ = $(\begin{matrix} -9 \\ 9 \\ 4 \end{matrix}) + 1 \cdot (\begin{matrix} 2 \\ -4 \\ -6 \end{matrix})$ = $(\begin{matrix} -7 \\ 5 \\ -2 \end{matrix})$

Die beiden Lösungspunkte sind also P₁ $(-3 | -3 | -14)$ und P₂ $(-7 | 5 | -2)$

Punkt auf Gerade, dass BCA 90°

Beispiel:

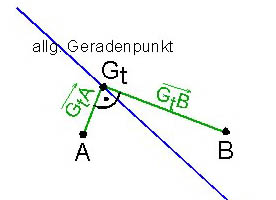Bestimme einen Punkt C (und einen Punkt C') auf der Geraden g mit g: $\vec{x} =$ $(\begin{matrix} -1 \\ -3 \\ 3 \end{matrix}) + t \cdot (\begin{matrix} 3 \\ 5 \\ -1 \end{matrix})$ , so dass das Dreieck ABC (ABC') mit A $(2 | 4 | -1)$ und B $(5 | 5 | 4)$ einen rechten Winkel in C (in C') hat.

Lösung einblenden

Da C auf der Geraden liegen muss, können wir C als allgemeinen Geradenpunkt $G_{t} (-1 + 3 t | -3 + 5 t | 3 - 1 t)$ auffassen. Die Verbindungsvektoren von C zu A und B sind also $\vec{G_{t}A}$ = $(\begin{matrix} 2 \\ 4 \\ -1 \end{matrix})$ - $(\begin{matrix} -1 + 3 t \\ -3 + 5 t \\ 3 - 1 t \end{matrix})$ = $(\begin{matrix} 3 - 3 t \\ 7 - 5 t \\ -4 + 1 t \end{matrix})$ und $\vec{G_{t}B}$ = $(\begin{matrix} 5 \\ 5 \\ 4 \end{matrix})$ - $(\begin{matrix} -1 + 3 t \\ -3 + 5 t \\ 3 - 1 t \end{matrix})$ = $(\begin{matrix} 6 - 3 t \\ 8 - 5 t \\ 1 + 1 t \end{matrix})$ .

Diese beiden Verbindungsvektor müssen orthogonal sein, um den rechten Winkel im C zu erhalten. Es muss also gelten:

$(\begin{matrix} 3 - 3 t \\ 7 - 5 t \\ -4 + 1 t \end{matrix})$ ⋅ $(\begin{matrix} 6 - 3 t \\ 8 - 5 t \\ 1 + 1 t \end{matrix})$ = 0

$(3-3t)\cdot(6-3t)+(7-5t)\cdot(8-5t)+(-4+1t)\cdot(1+1t) = 0$

$(9 t^{2}-27 t +18) + (25 t^{2}-75 t +56) + (1 t^{2}-3 t -4) = 0$

$35 t^{2} - 105 t +70 = 0$

t_1/2 = $\frac{+105 \pm \sqrt{{(-105)}^{2}-4\cdot35\cdot70}}{2 \cdot 35}$ = $\frac{+105 \pm \sqrt{1225}}{70}$ = $\frac{+105 ± 35}{70}$

t₁ = $\frac{70}{70}$ = $1$

t₂ = $\frac{140}{70}$ = $2$

t₁ eingesetzt in die Geradengleichung: $\vec{OC}$ = $(\begin{matrix} -1 \\ -3 \\ 3 \end{matrix}) + 1 \cdot (\begin{matrix} 3 \\ 5 \\ -1 \end{matrix})$ = $(\begin{matrix} 2 \\ 2 \\ 2 \end{matrix})$

t₂ eingesetzt in die Geradengleichung: $\vec{OC'}$ = $(\begin{matrix} -1 \\ -3 \\ 3 \end{matrix}) + 2 \cdot (\begin{matrix} 3 \\ 5 \\ -1 \end{matrix})$ = $(\begin{matrix} 5 \\ 7 \\ 1 \end{matrix})$

Die beiden Lösungspunkte sind also C $(2 | 2 | 2)$ und C' $(5 | 7 | 1)$

Probe:

$\vec{AC}$ ⋅ $\vec{BC}$ = $(\begin{matrix} 0 \\ -2 \\ 3 \end{matrix})$ ⋅ $(\begin{matrix} -3 \\ -3 \\ -2 \end{matrix})$ = $0 \cdot (-3) + (-2) \cdot (-3) + 3 \cdot (-2)$ = 0

$\vec{AC'}$ ⋅ $\vec{BC'}$ = $(\begin{matrix} 3 \\ 3 \\ 2 \end{matrix})$ ⋅ $(\begin{matrix} 0 \\ 2 \\ -3 \end{matrix})$ = $3 \cdot 0 + 3 \cdot 2 + 2 \cdot (-3)$ = 0

Einen Punkt an einer Geraden spiegeln (LF)

Beispiel:

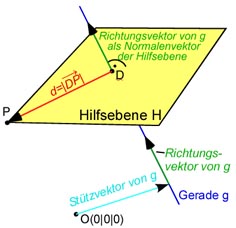Spiegle den Punkt P $(-2 | 6 | 0)$ an der Geraden g: $\vec{x} =$ $(\begin{matrix} 10 \\ 5 \\ 13 \end{matrix}) + t \cdot (\begin{matrix} 6 \\ 2 \\ 15 \end{matrix})$

Lösung einblenden

Um den Punkt an der Geraden zu spiegeln, brauchen wir den Lotfußpunkt von P an der Geraden, an dem der Punkt ja eigentlich gespiegelt wird. Diesen Lotfußpunkt bestimmen wir mit einer Hilfsebene.
Diese Hilfsebene ist orthogonal zu unserer Geraden

\vec{x} =

(\begin{matrix} 10 \\ 5 \\ 13 \end{matrix}) + t \cdot (\begin{matrix} 6 \\ 2 \\ 15 \end{matrix})

und enthält unseren Punkt P

(-2 | 6 | 0)

.
Der Normalenvektor der Hilfsebene ist also der Richtungsvektor der Geraden,

(\begin{matrix} 6 \\ 2 \\ 15 \end{matrix})

. Die Hilfsebene in der Koordinatenform ist somit

6 x_{1} + 2 x_{2} + 15 x_{3} = 0

Nun berechnen wir den Durchstoßpunkt der Geraden mit der Hilfsebene.

Gesucht ist der Durchstoßpunkt zwischen der Geraden g: $\vec{x} =$ $(\begin{matrix} 10 \\ 5 \\ 13 \end{matrix}) + t \cdot (\begin{matrix} 6 \\ 2 \\ 15 \end{matrix})$ und der Ebene E : $6 x_{1} + 2 x_{2} + 15 x_{3} = 0$ .

Wir setzen einen allgemeinen Geradenpunkt der Geraden $G_{t} (10 + 6 t | 5 + 2 t | 13 + 15 t)$ in die Ebene ein und lösen nach t auf:

$6 \cdot (10 + 6 t) + 2 \cdot (5 + 2 t) + 15 \cdot (13 + 15 t)$	=	0
$36 t + 60 + 4 t + 10 + 225 t + 195$	=	0
$265 t + 265$	=	0	\| $- 265$
$265 t$	=	$- 265$	\|: $265$
$t$	=	$- 1$

Den Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt $G_{t} (10 + 6 t | 5 + 2 t | 13 + 15 t)$ einsetzen.
=> D $(4 | 3 | -2)$ .

Dies ist der benötigte Lotfußpunkt

L (4 | 3 | -2)

.

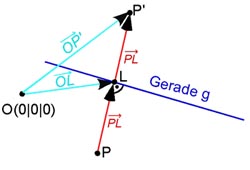Der Verbindungsvektor

\vec{PL}

zwischen dem zu spiegelnden Punkt P und diesem Lotfußpunkt

L (4 | 3 | -2)

ist der gleiche wie zwischen Lotfußpunkt und gesuchtem Bildpunkt P'. Addiert man diesen Verbindungsvektor zum Ortsvektor des Lotfußpunktes L,

\vec{OP'}

=

\vec{OL}

+

\vec{PL}

=

(\begin{matrix} 4 \\ 3 \\ -2 \end{matrix})

+

(\begin{matrix} 6 \\ -3 \\ -2 \end{matrix})

=

(\begin{matrix} 10 \\ 0 \\ -4 \end{matrix})

so erhält man den Ortsvektor des gespiegelten Bildpunktes P'.
Der gesuchte Spiegelpunkt ist also

P' (10 | 0 | -4)

Aufgabenbeispiele von Anwendungsaufgaben

Durchstosspunkt Anwendungen

Einen Punkt an einer Ebene spiegeln

Spiegel-Ebene zu zwei Punkten finden

Gerade an Ebene spiegeln

Geradenpunkt mit d zu Ebene finden

Punkt auf Gerade, dass BCA 90°

Einen Punkt an einer Geraden spiegeln (LF)