Aufgabenbeispiele von Gegenseitige Lagen - Schnitte
Durch Aktualisieren des Browsers (z.B. mit Taste F5) kann man neue Beispielaufgaben sehen
Durchstosspunkt zwischen Ebene und Gerade
Beispiel:
Berechne den Durchstoßpunkt der Geraden g: mit der Ebene E: .
Gesucht ist der Durchstoßpunkt zwischen der Geraden g: und der Ebene E :.
Wir setzen einen allgemeinen Geradenpunkt der Geraden in die Ebene ein und lösen nach t auf:
| = | |||
| = | |||
| = | | | ||
| = | |:() | ||
| = |
Den Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt
einsetzen.
=> D.
Gegenseitige Lage von Gerade und Ebene
Beispiel:
Untersuche die gegenseitige Lage der Gerade
g: mit der Ebene E:Berechne ggf. Abstand bzw. Durchstoßpunkt.
Um die gegenseitige Lage der Gerade und der Ebene zu überprüfen, bilden wir das Skalarprodukt aus dem Normalenvektor der Ebene und dem Richtungsvektor der Geraden.
=-4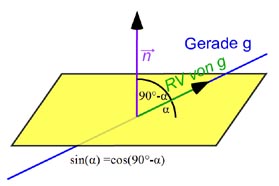 Da das Skalarprodukt ungleich null ist, sind der Normalenvektor
der Ebene und der Richtungsvektor der Geraden nicht orthogonal zueinander; somit haben Ebene und Gerade einen gemeinsamen
Punkt, den Durchstoßpunkt. Diesen berechnen wir jetzt.
Da das Skalarprodukt ungleich null ist, sind der Normalenvektor
der Ebene und der Richtungsvektor der Geraden nicht orthogonal zueinander; somit haben Ebene und Gerade einen gemeinsamen
Punkt, den Durchstoßpunkt. Diesen berechnen wir jetzt.
Gesucht ist der Durchstoßpunkt zwischen der Geraden g: und der Ebene E :.
Wir setzen einen allgemeinen Geradenpunkt der Geraden in die Ebene ein und lösen nach t auf:
| = | |||
| = | |||
| = | | | ||
| = | |:() | ||
| = |
Den Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt
einsetzen.
=> D.
Gegenseitige Lage zweier Ebenen (LF)
Beispiel:
Untersuche die gegenseitige Lage der beiden Ebenen
E: und F:Berechne ggf. Abstand bzw. Schnittgerade.
Für die beiden Normalenvektoren der Ebenen gilt:
Die Normalenvektoren sind somit linear abhängig, daher müssen die beiden Ebenen parallel oder identisch sein.
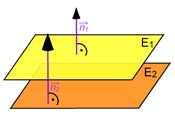 In diesem Fall sind sie nicht identisch, sondern parallel:
Es gibt keinen Faktor, mit welchem man die Gleichung der einen Ebene auf die Gleichung der anderen Ebene bringen kann.
In diesem Fall sind sie nicht identisch, sondern parallel:
Es gibt keinen Faktor, mit welchem man die Gleichung der einen Ebene auf die Gleichung der anderen Ebene bringen kann.
Um den Abstand der parallelen Ebenen zu berechnen, genügt es den Abstand eines beliebigen Punktes auf F z.B. S1 zur Ebene E zu berechnen:
Wir berechnen den Abstand zwischen Punkt und Ebene mittels der Hesse'schen Normalenform.
= 7
Gegenseitige Lage zweier Ebenen (BF)
Beispiel:
Untersuche die gegenseitige Lage der beiden Ebenen
E: und F:Berechne ggf. den Abstand.
Die beiden Normalenvektoren und der Ebenen sind linear unabhängig (keine Vielfachen). Die Ebenen sind somit nicht parallel, also schneiden sich die Ebenen.
Gegenseitige Lage zweier Geraden (+Abstände)
Beispiel:
Untersuche die gegenseitige Lage der beiden Geraden
g: und h:Berechne ggf. Abstand bzw. Schnittpunkt.
Die beiden Richtungsvektoren und der Geraden
sind keine Vielfachen voneinander, die Geraden können also weder parallel noch identisch sein. Wir müssen deswegen
noch prüfen, ob die Geraden einen Schnittpunkt haben oder nicht.
Wir setzen dazu die beiden Geraden gleich und lösen das so entstehende Lineare Gleichungssystem.
=
langsame Rechnung einblenden
langsame Rechnung einblenden
Es gibt also kein s und t für die alle 3 Gleichungen und damit die ursprüngliche Vektorgleichung erfüllt sind.
Die Geraden sind also windschief.Berechnung des Abstands der windschiefen Geraden.
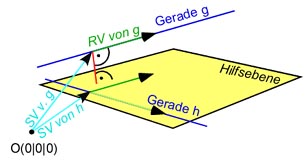 Zuerst bilden wir eine Ebene, welche die Gerade h:
Zuerst bilden wir eine Ebene, welche die Gerade h:
Der Normalenvektor dieser Ebene ist der Normalenvektor auf die beiden Richtungsvektoren der Geraden.
Wenn wir den Aufpunkt von h Ah
Nun können wir den Abstand zwischen der Geraden g:
Wir berechnen den Abstand zwischen Punkt und Ebene mittels der Hesse'schen Normalenform.
Mittelebene zu 2 parallelen Ebenen
Beispiel:
Gegeben sind zwei zueinander parallele Ebenen E1:
 Die Normalenvektoren von E1 und E2 sind linear abhängig, also sind sie parallel. Da
auch die Ebene F dazu parallel sein soll, muss auch deren Normalenvektor dazu linear abhängig sein, z.B.
Die Normalenvektoren von E1 und E2 sind linear abhängig, also sind sie parallel. Da
auch die Ebene F dazu parallel sein soll, muss auch deren Normalenvektor dazu linear abhängig sein, z.B.
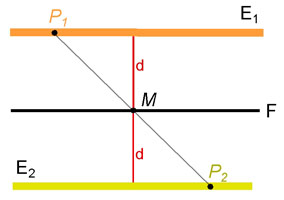
Anhand der Skizze erkennt man, dass wegen des Strahlensatzes der Mittelpunkt zwischen zwei beliebigen Punkten von E1 und E2 diese Bedingung erfüllt.
Wir wählen als beliebige Punkte von E1 den Punkt P1
Punktprobe mit M in F ergibt für d=
Die gesuchte Ebene ist also F:
Schnittgerade zweier Ebenen berechnen (LF)
Beispiel:
Berechne die Schnittgerade der beiden Ebenen
E1:
 Wir schreiben die beiden Ebenen als LGS untereinander
Wir schreiben die beiden Ebenen als LGS untereinander(1)
(2)
1⋅(1)-1⋅(2)
(1)(2)
setze x3 = t
-1x2 = 2 - 3⋅t |:-1
x2 = -2
eingesetzt in (1):
1x1 +1⋅(-21x1
1x1
1x1 =
x1 =2
x1 = 2
x2 = -2
x3 =
Die gesuchte Schnittgerade ist also :
Weil der Richtungsvektor ja immer in der Geraden drin liegt, darf man diesen (im Gegensatz zum Stützvektor) mit jeder Zahl durchmultiplizieren, also auch mit 1:
Lotfußpunkt einer Ebene zu P
Beispiel:
Bestimme den Lotfußpunkt des Punktes P
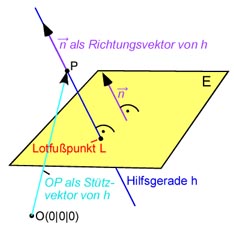 Der Normalenvektor der Ebene ist:
Der Normalenvektor der Ebene ist:
Wir bilden eine Gerade mit diesem Normalenvektor als Richtungsvektor, welche durch unseren Punkt
Nun berechnen wir den Durchstoßpunkt dieser Geraden mit unserer Ebene E:
Gesucht ist der Durchstoßpunkt zwischen der Geraden g:
Wir setzen einen allgemeinen Geradenpunkt der Geraden
|
|
= |
|
|
|
|
= |
|
|
|
|
= |
|
|
|
|
|
= |
|
|: |
|
|
= |
|
Den Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt
=> D
Dieser Durchstoßpunkt D ist der gesuchte Lotfußpunkt L

